Análisis de pruebas diagnósticas (II): Reproductibilidad con variables cuantitativas y comparabilidad de dos métodos analíticos

Introducción

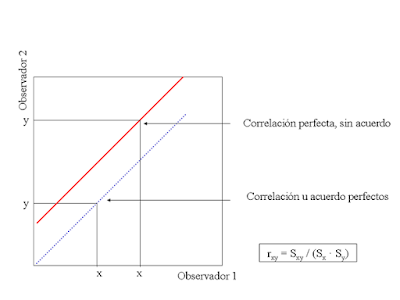
En un artículo previo se trató la manera en que debe analizarse la reproductibilidad de pruebas diagnósticas cuando la variable medida se trataba de una de tipo cualitativo (por ejemplo positivo/negativo, escalas de ordenación, etc). En el presente artículo se estudiará la manera en que deberíamos hacerlo cuando se trata de variables cuantitativas. En estos casos podemos analizar la consistencia interna de la prueba (mediante el coeficiente de correlación intraclase de consistencia), y del acuerdo entre observadores (mediante la determinación del coeficiente de correlación intraclase de acuerdo o mediante métodos gráficos).
Dos errores frecuentes a la hora de valorar la reproductibilidad de este tipo de pruebas es recurrir al coeficiente de correlación o a la T de Student pareada. Debemos recordar que el coeficiente de correlación determina si la nube de puntos que generan las determinaciones de dos observadores se ajusta bien a una recta. De esta manera dos observadores pueden generar una nube de puntos que se ajuste de forma perfecta a una recta (r = 1), y que exista o no acuerdo entre ellos. Lo vemos en la siguiente figura. La línea de puntos azul se corresponde con dos observadores con acuerdo perfecto (x siempre es igual a y); por el contrario la línea roja, con una correlación también perfecta, no presenta acuerdo entre observadores.

Por su parte la T de Student pareada es una prueba paramétrica y está basada en la media y error estándar de las diferencias de medición entre dos observadores, siendo la hipótesis nula que la media de diferencias es 0. La prueba tiene como limitación que cuanto mayor sean las diferencias en valor absoluto mayor será el error estándar y más difícil será encontrar significación para un mismo tamaño muestral. Hay que recordar para entender esto, que el rechazo de la hipótesis nula se basa en encontrar un valor absoluto de z mayor que 1,96 para una confianza del 95% en la fórmula

Al aumentar las diferencias y aumentar el error estándar manteniendo fijos los demás parámetros z se hace menor pues aumenta el denominador.

Reproductibilidad

Coeficientes de correlación intraclase

El método más adecuado para analizar la reproductibilidad en esta situación es la determinación de los coeficientes de correlación intraclase (CCI). Supongamos el siguiente ejemplo sobre la determinación de la glucemia capilar en 10 sujetos con 5 observadores:

Determinación de la glucemia capilar en 10 sujetos por 5 observadores

	Observador 1	Observador 2	Observador 3	Observador 4	Observador 5
1	155	157	165	162	163
2	230	225	240	225	218
3	175	184	185	181	190
4	300	297	310	295	290
5	235	230	245	230	225
6	125	132	135	132	139
7	130	125	140	135	130
8	189	184	199	184	179
9	291	296	301	296	301
10	305	310	315	295	300
Media	213,5	214	223,5	213,5	213,5
Varianza	4290,45	4290	4290,45	3787,85	3795,85

La variabilidad total en las mediciones realizadas por los cinco observadores sobre las mismas muestras puede ser debida a la diferencia existente entre las muestras correspondientes a 10 sujetos diferentes y a la variabilidad de la medición realizada por los 5 observadores, y ésta última a su vez puede descomponerse en una variabilidad debida a la medición y la variabilidad debida al azar. De esta forma, y sólo con ánimo de ilustrar y no de formular modos de cálculo, los CCI podrían representarse de la siguiente forma:

• CCI de consistencia (CCIc): Tiene en cuenta la variabilidad debida al los sujetos de estudio y la debida al azar, no teniendo en cuenta la variabilidad debida a los observadores. Se mide por tanto el comportamiento de la prueba en los sujetos de estudio.
  
  
• CCI de acuerdo (CCIa): Tiene en cuenta la variabilidad debida al los sujetos de estudio, la debida al azar, y la debida a los observadores
  
  

El cálculo realmente lo podemos hacer a través de la tabla de suma de cuadrados y cuadrados medios de un modelo de ANOVA de 1 factor con medidas repetidas. Cada componente de variación viene dado por su cuadrado medio (suma de cuadrados dividido por los grados de libertad de cada componente, que para la variabilidad por los sujetos es N-1 [variabilidad intragrupo], para la debida a los observadores es O-1 [variabilidad intergrupo], y para la debida al azar es (N-1) x (O-1)). De esto debemos inducir que para el cálculo de los CCI deben cumplirse las premisas necesarias para plantear cualquier ANOVA:

• Normalidad
• Homocedasticidad (varianzas homogéneas)
• Independencia

El CCIc sólo detecta disparidad causada por diferencias proporcionales, mientras que el CCIa detecta cualquier tipo de disparidad, ya sea aditiva o proporcional. Respecto a la interpretación de los resultados, un CCI < 0,4 implica baja fiabilidad, entre 0,4 y 0,75 moderada fiabilidad y >0,75 buena fiabilidad (existiendo también otras clasificaciones). Cuando las mediciones son idénticas para cada observador, los CCI valen exactamente 1.
Volviendo al ejemplo, entre los observadores 1 y 2 no encontramos diferencias en la media ni en la varianza, por lo que probablemente no exista variabilidad interobservador y CCIc y CCIa tendrán un valor similar. Ocurre lo mismo con los observadores 4 y 5, pero en este caso la varianza es menor, por lo que el numerador de los CCI también será menor así como su resultado final: los CCI son muy dependientes de la variabilidad en la medición en una población concreta además del azar, pudiendo no ser comparables CCI hallados a partir de diferentes poblaciones. Entre los observadores 1 y 3 hay diferencias de media pero no de varianza (en este caso porque el segundo siempre encuentra valores superiores al primero). Los observadores no son comparables mediante CCI pues las varianzas no son homogéneas.
Para el cálculo de los CCI procederemos al cálculo de las tablas correspondeintes de un ANOVA de un factor con muestras repetidas. En el caso del ejemplo expuesto:

Tabla ANOVA

	O1	O2	O3	Medias	Cuadrados
1	155	157	165	159	(159 - 217)2 = 3364
2	230	225	240	231,66	(231,66 - 217)2 = 215,11
3	175	184	185	181,33	1272,11
4	300	297	310	302,33	7281,11
5	235	230	245	236,66	386,77
6	125	132	135	130,66	7453,44
7	130	125	140	131,66	7281,77
8	189	184	199	190,66	693,44
9	291	296	301	296	6241
10	305	310	315	310	8649
Medias	213,5	214	223,5	217	suma x 10 filas = 128515,33
Cuadrados	(213,5 - 217)2= 12,25	(214 - 217)2 = 9	(223,5 - 217)2 = 42,25	suma x 3 columnas = 635

Para hallar la suma de cuadrados de la interacción, es decir, la correspondiente al azar, hay que crear una nueva tabla en la que a cada valor se le resta la media global (o media de totas las medias) y la diferencia de la media de su fila y columna respecto a la media global, y ese valor se eleva al cuadrado; esto es, por ejemplo para el valor de la primera fila y columna: 155 - (217 + [159-217] + [213,5-217]) = -0,5² = 0,25 (en esta formulación el término que se le sustrae a 155 es el valor esperado para esa casilla de acuerdo con el modelo planteado). Por último se suman todos estos valores. Para nuestro ejemplo dicha suma de cuadrados es 193,67.
Nos queda plantear la tabla resumen:

Resumen de resultados

	Suma de cuadrados	gdl	Cuadrados medios (SC/gdl)	CCIc	CCIa
Observadores	635	3-1 = 2	317,5	0,99	0,99
Sujetos	128515,33	10-1 = 9	14279,48
Azar	193,67	2 x 9 = 18	10,76
Total	129344	29

Por tanto entre los 3 observadores existe una buena consistencia y acuerdo.

Métodos gráficos

Otra forma de analizar el grado de acuerdo entre dos fuentes de medidas es el métodp gráfico de Altman y Bland, que tiene como requisito que las mediciones se distribuyan según una distribución normal. Se trata de un gráfico de nube de puntos contruido a partir de parejas de mediciones de dos observadores; cada X se corresponde con la media de las dos mediciones, y su correspondiente Y es su diferencia. El acuerdo perfecto vendrá dado por la coincidencia entre la recta de regresión de la nube de puntos y el eje X (panel A, CCIc = CCIa = 0,99); una recta paralela al eje X indica consistencia pero desacuerdo por diferencia aditiva constante entre los dos observadores (panel B, CCIc = 1, CCIa = 0,98); por el contrario una recta de regresión con pendiente refleja una relación entre la medición y el grado de desacuerdo entre los observadores (diferencia proporcional al valor absoluto de la medición) (paneles C y D).

Comparación de dos métodos analíticos

En ocasiones podemos necesitar analizar si existen errores sistemáticos en las determinaciones de dos sistemas de medida diferentes. Supongamos que tenemos dos métodos A y B, podríamos teorizar que las medidas realizadas con el método A son

donde α representa las diferencias aditivas, β las diferencias proporcionales y ε el error aleatorio. Siempre que α = 0 y β = 1, los métodos A y B serán comparables. Dado que A y B no están exentos de error, no es posible utilizar la regresión lineal simple. Para ello recurrimos a determinar la recta de regresión mediante dos posibles métodos:

• Método de Deming (paramétrico, supone normalidad y homogeneidad de varianzas):
  
• Método de Passing y Bablock (no paramétrico): Es el método de lección. Se obtienen todas los posibles puntos formados por las N mediciones de A y B; luego se determinan todas las posibles parejas de puntos (½ N x [N-1] parejas); cada pareja de puntos formará una recta de la que determinaremos su pendiente ([A_i-A_j]/[B_i-B_j]); para cada pareja de puntos y a partir de la pendiente hallada determinaremos su ordenada en el origen(o_i = A_i - p_i x B_i); β será la mediana de todas las pendientes mayores de -1; α será la mediana de las ordenadas en origen.

Ambos métodos poseen sus metodologías para el cálculo de los correspondientes intervalos de confianza para comprobar si existe diferencia estadísticamente significativa de α respecto de 0 y β respecto de 1, y concluir así si ambos métodos son o no comparables.

Ficha bibliográfica

Título:

Análisis de pruebas diagnósticas (II): Reproductibilidad con variables cualitativas y comparabilidad de dos métodos analíticos

Dirección:

http://epidemiologia-estadistica.blogspot.com.es/2013/02/analisis-de-pruebas-diagnosticas-ii.html

Descripción:

Se estudian los índices con los que puede analizarse la reproductibilidad de una prueba diagnóstica y su interpretación, cuando dicha prueba nos ofrece el resultado en forma de una variable cuantitativa.

Palabras clave:

reproductibilidad, validez, pruebas diagnósticas

Código de idioma:

es

Autor/a:

Fco. Javier Caballero Granado

Editor/a:

Fco. Javier Caballero Granado

Derechos:

Fco. Javier Caballero Granado

Fecha de creación:

2010-11-03

Fecha de modificación:

2010-11-10

Forma parte de:

Notas sobre estadística

Cómo citar:

Caballero-Granado FJ. Análisis de pruebas diagnósticas (II): Reproductibilidad con variables cualitativas y comparabilidad de dos métodos analíticos [en línea]. Sociedad Andaluza de Enfermedades Infecciosas Ed. Creado el 03/11/2010; actualizado el 2010-11-10 . Disponible en web: http://epidemiologia-estadistica.blogspot.com.es/2013/02/analisis-de-pruebas-diagnosticas-ii.html [consultado el ...]

Análisis de pruebas diagnósticas (I): reproductibilidad de variables cualitativas

Introducción

Una buena parte de nuestra labor como médicos es realizar mediciones e interpretar el resultado de estas mediciones. Al realizar mediciones debemos ser conscientes de la variabilidad que entreñan: el resultado de una medición va estar condicionado por:

• Las características de la población en la que la realizamos (características demográficas, clínicas, genéticas, ...)
• Las características de la enfermedad en la que aplicamos la medición (puede haber diferencias según el estadio en el que se encuentre)
• El propio proceso de la medición (puede existir error aleatorio, distintos criterios de interpretación, aparataje diferente, ...)

Para evaluar la bondad o precisión (accuracy) de una medición, o de una prueba diagnóstica, existe toda una serie de técnicas estadísticas, y de ellas es de lo que aquí vamos a tratar. Y en concreto de la variabilidad en la medición derivada del propio proceso de medición.
Esta variabilidad la aquilataremos mediante el análisis de dos aspectos:

• La reproductibilidad (agreement, reproductibility, reliability), que puede ser interobservador o intraobservador
• La validez (validity)
  • Interna, que estudia el grado en el que los resultados observados se deben a una intervención realizada (factores de confusión, sesgo de selección, tamaño muestral, ...)
  • Externa, que estudia en qué grado los resultados obtenidos pueden generalizarse a poblaciones y situaciones espaciotemporales diferentes a las consideradas en el estudio

Reproductibilidad

Tal como vemos en el siguiente esquema, disponemos de diversas pruebas para evaluar la reproductibilidad de una prueba diagnóstica según el tipo de variable que se esté midiendo.

Figura 1

Supongamos que disponemos de una prueba que es capaz de determinar la positividad o negatividad respecto del diagnóstico de una determinada enfermedad. Deseamos conocer en qué grado se obtienen los mismos resultados cuando dos observadores diferentes aplican la prueba a los mismos 100 enfermos (aunque este mismo planteamiento es el que se podría realizar cuando un mismo observador repite varias veces la prueba en cada enfermo). Para ello anotaremos los casos en los que ambos observadores llegan a un acuerdo en positividades y en negatividades y aquellos otros casos en los que existe discrepancia, así:

Tabla 1: Acuerdo interobservador en 100 pacientes

		Observador 1
O b s e r v a d o r 2		+	-	total
	+	40a	5b	45
	-	10c	45d	55
	total	50	50	100

Como vemos cada uno de ellos habrá realizado 100 mediciones (es decir, entre ambos habrán realizado 200 mediciones). En esta situación podemos decir que 40 mediciones positivas del observador 1 coinciden con 40 mediciones positivas del observador 2 (80 mediciones), de un total de mediciones positivas de 50 del observador 1 y 45 del observador 2 (95 mediciones). El cociente entre ambas cifras (80/95 = 0.84) es lo que llamamos el índice de acuerdo específico de positividades (P₀₊).

Podemos hacer el mismo cálculo con las negatividades: 90/105 = 0.86; en este caso hablamos del índice de acuerdo específico de negatividades (P_0-). 

Cada uno de estos índices nos habla de la reproductibilidad de la prueba para positividades y negatividades. Sus valores oscilan entre 0 y 1, e índices cercanos a 1 implican buena reproductibilidad.

También podemos considerar el número de parejas de determinaciones en las que existe acuerdo, ya sea de positividad o de negatividad; en el ejemplo de la Tabla 1, 40 + 45 / 100 = 0.95. En este caso hablamos del índice de acuerdo total (P₀).
Estos índices de forma aislada tienen escaso valor, ya que pueden existir situaciones con buen acuerdo total y uno de los índices de acuerdo específico muy malo. Un ejemplo lo tenemos en la Tabla 2.

Tabla 2: Acuerdo interobservador en 100 pacientes con mal acuerdo específico y buen acuerdo total

		Observador 1
O b s e r v a d o r 2		+	-	total
	+	90	5	95
	-	5	0	5
	total	95	5	100

Observemos ahora la Tabla 1 y 2 desde otra perspectiva. La diagonal formada por las dos celdas correspondientes a las discordancias (b y c), nos habla de asimetrías entre los dos observadores en la tendencia hacia la positividad o la negatividad en la interpretación del resultado de la prueba. Si esta asimetría es considerablemente grande nos informa de que un observador tiende a dar uno de los posibles resultados más frecuentemente que el otro observador. Esto lo podemos plasmar numéricamente mediante el índice de sesgo de McNemar (S_McN), y viene expresado por el cociente entre el valor absoluto de la diferencia de desacuerdos en el numerador y la suma de desacuerdos en el denominador.

En el ejemplo de la Tabla 1, (10 - 5) / (10 + 5) = 0.33; para la Tabla 2, (5 - 5) / (5 + 5) = 0. Por este segundo ejemplo podemos ver que la existencia de simetría completa es un dato más, pero igual que antes por sí solo es un mal índice; de forma recíproca, los índices de acuerdo pueden ser muy buenos y presentar un sesgo importante (Tabla 3: P₀₊ = 0.88; P_0- = 0.90; P₀ = 0.89; S_McN = 0.82) .

Tabla 3: Acuerdo interobservador en 100 pacientes con buen acuerdo y sesgo importante

		Observador 1
O b s e r v a d o r 2		+	-	total
	+	40	1	41
	-	10	49	59
	total	50	50	100

Un último índice es el índice kappa (κ); se trata de una medición del grado de acuerdo entre observadores después de detraerle el posible acuerdo que puede achacarse sólo al azar. Dicho de otra manera, es el cociente entre el exceso de acuerdo respecto del azar en el numerador, y el máximo exceso de acuerdo posible respecto al debido al azar en el denominador. Para su cálculo necesitamos las frecuencias de cada celda, en vez de sus valores absolutos. En la Tabla 4 hemos transformado la Tabla 1:

Tabla 4: Acuerdo interobservador en 100 pacientes

		Observador 1
O b s e r v a d o r 2		+	-	total
	+	0.4	0.05	0.45
	-	0.1	0.45	0.55
	total	0.5	0.5	1

El acuerdo total (F₀) será 0.4 (positividades) más 0.45 (negatividades), 0.85. El azar (F_e) podría explicar 0.45 (total de positividades del observador 2) por 0.5 (total de positividades del observador 1), más 0.55 (total de negatividades del observador 2) por 0.5 (total de negatividades del observador 2).

En nuestro ejemplo de la Tabla 4, κ toma un valor de

Este índice puede tomar valores entre -1 y +1. κ = 0 implica que se ha obtenido el mismo acuerdo entre observadores que podría esperarse por el azar. La interpretación de κ podemos verla en las Tablas 5 y 6:

Tabla 5: Interpretación de kappa por Fleiss

Rango	Categoría
> 0.75	Excelente
0.4 - 0.75	Moderado
< 0.4	Pobre

Tabla 6: Interpretación de kappa por Landis y Koch

Rango	Categoría
> 0.8	Muy bueno
0.61 - 0.8	Bueno
0.41 - 0.6	Moderado
0.21 - 0.4	Bajo
< 0.21	Pobre
≤ 0	Sin acuerdo

El índice κ puede generalizarse para más de dos categorías (Figura 2); en ese caso F₀ vendría dada por la suma de frecuencias de acuerdo en las distintas categorías (en la Figura 2, F₁₁+F₂₂+F₃₃) y F_e por la suma de productos de los correspondientes totales marginales para ambos observadores (F_1· x C_·1 + F_2· x C_·2 + F_3· x C_·3).

Figura 2

Por último, si la variable es cualitativa ordinal (las diferentes categorías guardan un orden determinado), puede emplearse el índice κ ponderado. El cálculo es similar, pero el valor de cada celda de la tabla es ponderado por un valor (un peso). Este peso podría asignarse de forma arbitraría, pero existen métodos que hacen esta tarea de una forma más correcta, ya que la asignación arbitraría de pesos llevaría a la imposibilidad de comparación de varios índices κ. Estos métodos son el método cuadrático y el método de errores absolutos. Veámoslo con un ejemplo en la Tabla 7A.

Tabla 7A: Medición del grado de disnea según la clasificación de la NYHA entre dos observadores

Grado de disnea	I-II	III	IV
I-II	15	5	3	23
III	5	20	10	35
IV	2	10	30	42
	22	35	43	100

Si llamamos:

• r, al número de categorías
• i, al número de orden de la categoría que nos ocupe de un observador
• j, al número de orden de la categoría que nos ocupe del otro observador
• w_ij, al peso que le corresponde a la celda de la categoría i del primer observador y la categoría j del segundo onservador

el peso que le corresponderá a cada celda vendrá dado por

• Método cuadrático:
  
  
• Método de errores absolutos:
  
  

Tabla 7B: Medición del grado de disnea según la clasificación de la NYHA entre dos observadores

Grado de disnea	I-II	III	IV
I-II	[1] / (1)	[0.75] / (0.5)	[0] / (0)
III	[0.75] / (0.5)	[1] / (1)	[0.75] / (0.5)
IV	[0] / (0)	[0.75] / (0.5)	[1] / (1)

La Tabla 7B muestra las ponderaciones para cada celda por el método cuadrático (con corchetes) y de errores absolutos (con paréntesis). Ahora sólo nos quedaría multiplicar en cada celda su frecuencia relativa (el valor que aparece en la Tabla 7A dividido por el total de mediciones), por el peso que le ha correspondido por uno u otro método. En la Tabla 7C observamos el resultado con los pesos cuadráticos:

Tabla 7C: Medición del grado de disnea según la clasificación de la NYHA entre dos observadores

Grado de disnea	I-II	III	IV
I-II	0.15 x 1	0.05 x 0.75	0.03 x 0	0.23
III	0.05 x 0.75	0.2 x 1	0.1 x 0.75	0.35
IV	0.02 x 0	0.1 x 0.75	0.3 x 1	0.42
	0.22	0.35	0.43	1

En esta situación F₀ es la suma de todas las celdas ya ponderadas. Y F_e sería la suma de productos de los correspondientes totales marginales para cada celda, ponderándolos por el peso correspondiente a dicha celda (en nuestro ejemplo y para la primera fila: F_1· x C_·1 x w₁₁ + F_1· x C_·2 x w₁₂+ F_1· x C_·3 x w₁₃ = 0.23 x 0.22 x 1 + 0.23 x 0.35 x 0.75 + 0.23 x 0.43 x 0 = 0.11; para la segunda fila: 0.35 x 0.22 x 0.75 + 0.35 x 0.35 x 1 + 0.35 x 0.43 x 0.75 = 0.29; y para la tercera fila: 0.42 x 0.22 x 0 + 0.42 x 0.35 x 0.75 + 0.42 x 0.43 x 1 = 0.29). Así en esta ejemplo el valor de κ será:

El índice κ presenta una serie de limitaciones:

1. Su valor disminuye al aumentar el número de categorías del resultado de la prueba. Por tanto no son comparables índices κ de pruebas con diferente número de categorías. Por el contrario, en relación al índice κ ponderado y el uso de pesos cuadráticos, el valor del índice aumenta al aumentar el número de categorías.
2. Su valor se ve afectado por desequilibrios entre los totales marginales de la tabla (positividades y negatividades de ambos observadores), y esta influencia es tanto mayor cuanto mayor es el acuerdo total, por lo que κ debe facilitarse junto con los índices de acuerdo específico.
3. Su valor se ve afectado por la presencia de sesgo, de forma que cuando existen grandes sesgos el valor de κ se eleva. Esta influencia es tanto mayor cuanto menor es el valor de κ. Veamos el siguiente ejemplo:
   
   

   Tabla 8A: Influencia del sesgo en κ (sesgo elevado)

   		Observador 1
   O b s e r v a d o r 2		+	-	total
   	+	29	6	35
   	-	38	27	65
   	total	67	33	100

   
   En este ejemplo el índice de sesgo es |38 - 6| / (38 + 6) = 0.72, un sesgo elevado, arrojando un valor de κ de 0.2. Sin embargo, con índices de sesgo inferiores (0.04):
   
   

   Tabla 8B: Influencia del sesgo en κ (sesgo bajo)

   		Observador 1
   O b s e r v a d o r 2		+	-	total
   	+	29	21	50
   	-	23	27	50
   	total	52	48	100

   
   el valor de κ se reduce a 0.12.
4. Su valor se ve afectado por la prevalencia de la característica en la muestra en la que se realiza la prueba, de forma que con prevalencias muy elevadas o muy pequeñas (es decir, extremas), se obtendrá un índice κ de valor bajo. Esta influencia es tanto mayor cuanto mayor es el valor de κ. Por tanto, no son comparables índices κ procedentes de poblaciones muy diferentes respecto a la característica que se estudie.
   Para valorar la prevalencia de la característica estudiada suele usarse el índice de prevalencia, cociente entre el valor absoluto de la diferencia entre acuerdos de positividades y negatividades en el numerador y el total de pruebas realizadas en el denominador.
   
   
   
   
   Consideremos el siguiente ejemplo:
   

   Tabla 9A: Influencia de la prevalencia en κ (prevalencia elevada)

   		Observador 1
   O b s e r v a d o r 2		+	-	total
   	+	28	3	31
   	-	6	2	8
   	total	34	5	39

   
   Vemos que |28 - 2|/39 = 0.67, es un índice elevado. Esto hace la probabilidad de acuerdo simplemente por azar también elevada (F_e = 0.72), y por tanto que el índice κ sea bajo; en el ejemplo κ = 0.18. En cambio con prevalencias intermedias:
   
   

   Tabla 9B: Influencia de la prevalencia en κ (prevalencia intermedia)

   		Observador 1
   O b s e r v a d o r 2		+	-	total
   	+	15	3	18
   	-	6	15	21
   	total	21	18	39

   
   (índice de prevalencia 0, F_e = 0.5), el índice κ aumenta su valor (0.54).

Un último aspecto a tratar relacionado con el índice κ es su significación. Para ello construiremos su intervalo de confianza al 95% a partir de su error estándar:

siendo:

• r, el número de categorías
• F_e, el acuerdo esperado por el azar
• f_i , el total marginal de la fila
• c_i , el total marginal de la columna

El intervalo de confianza vendría dado por:

Volviendo al ejemplo inicial expresado en frecuencias (Tabla 4), F_e es 0.5, r = 2, n = 100, f₁·c₁·(f₁+c₁) = 0.21, f₂·c₂·(f₂+c₂) = 0.28, por lo que el ee(κ) = 0.09. El IC quedaría [-0.28 ; -0.10].

Ficha bibliográfica

Título:

Análisis de pruebas diagnósticas (I): reproductibilidad de variables cualitativas

Dirección:

http://epidemiologia-estadistica.blogspot.com.es/2013/02/analisis-de-pruebas-diagnosticas-i.html

Descripción:

Tras una breve introducción para definir conceptos relacionados con el análisis de pruebas diagnósticas, se estudian los índices con los que puede analizarse la reproductibilidad de una prueba diagnóstica y su interpretación.

Palabras clave:

reproductibilidad, validez, pruebas diagnósticas

Código de idioma:

es

Autor/a:

Fco. Javier Caballero Granado

Editor/a:

Fco. Javier Caballero Granado

Derechos:

Fco. Javier Caballero Granado

Fecha de creación:

2007-02-16

Fecha de modificación:

2010-10-31

Forma parte de:

Notas sobre estadística

Cómo citar:

Caballero-Granado FJ. Análisis de pruebas diagnósticas (I): reproductibilidad de variables cualitativas [en línea]. Caballero-Granado FJ Ed. Creado el 16/02/2007; actualizado el 2010-10-31. Disponible en web: http://epidemiologia-estadistica.blogspot.com.es/2013/02/analisis-de-pruebas-diagnosticas-i.html [consultado el ...]

Inferencia estadística según el modelo bayesiano

Ya vimos con anterioridad cómo en el modelo frecuentista el parámetro poblacional que se desea inferir (θ) es considerado una constante, mientras que se consideran aleatorios los datos obtenidos de la muestra (y), y por tanto el estadístico que se empleará para determinar el valor del parámetro poblacional. De esta forma el intervalo de confianza era definido como un rango de valores tal que, si repitiéramos infinidad de veces el experimento, el 95% de las estimaciones del parámetro poblacional estarían contenidas en él.

En el modelo bayesiano el planteamiento es radicalmente diferente:

• Lo que se considera constante es la información que se posee de la población, es decir, los datos (y)
• El parámetro poblacional que se desea estimar (θ) es considerado variable. En este sentido, ya no es necesaria la búsqueda de buenos estimadores, como ocurría en la estadística frecuentista.
• Para la estimación del parámetro poblacional es necesario un conocimiento previo de la distribución que pueda seguir el parámetro poblacional. Es lo que se llama distribución a priori.
• No se hace referencia a intervalo de confianza, sino a intervalo de credibilidad, que sería el intervalo que contendría al parámetro poblacional con una probabilidad del 95% (concepto muy usado, pero erróneo, para referirse al intervalo de confianza dentro de la estadística frecuentista).

Las estimaciones en el modelo de bayesiano se realizan basándose en el teorema de Bayes:

P(B|A) = P(A|B) · P(B) / P(A)

Una pieza fundamental de este modelo es el conocimiento a priori del parámetro que se quiere inferir. En este sentido, hay que decir que si bien θ es el parámetro que se desea estimar, siempre se tiene alguna información sobre él (ya sea una información subjetiva a través de la experiencia u objetiva a través de otro estudio previo) (Figura 1); y en caso contrario, siempre se prodrían realizar experimentos seriados que proporcionarían dicho conocimiento (Figura 2).

Componentes del modelo bayesiano

 



Figura 1

 

Figura 2

Para el modelo bayesiano esta experiencia previa es muy valiosa; por el contrario para el modelo frecuentista este conocimiento previo no tiene valor. Precisamente es este aspecto el más original pero también el más criticado del enfoque bayesiano: este conocimiento a priori podría ser "manipulado" para que los resultados del estudio sean convenientes. En este sentido, también el enfoque frecuentista tiene sus posibilidades de manipulación: es necesario prever un modelo con unos determinados errores tipo I y tipo II y predeterminar un tamaño muestral adecuado. El valor de p no es más que el resultado de un cálculo matemático directamente relacionado con el tamaño muestral: la significación estadística podría reducirse a la capacidad para aportar una muestra suficientemente grande. Por tanto el problema no se encontraría en el enfoque dado al estudio, sino en la poca honestidad de quien diseña el estudio.

Este conocimiento a priori se trata en resumen de una distribución de frecuencias, y como tal, con valores más frecuentes (dados por más probables por el investigador) y otros menos frecuentes (tenidos por menos probables por el investigador). La valoración de los distintos escenarios respecto a la información previa es lo que se conoce como análisis de sensibilidad. Dentro de esos posibles escenarios estaría aquel en el que no poseemos información previa (que se corresponde con una probabilidad a priori de 0.5 si se tratara de un suceso frente a su complementario).

Supongamos un estudio en el que se desea conocer la prevalencia de EPOC en una población, para lo que se entrevista a 170 personas. El investigador sostiene que lo más probable es que la prevalencia sea del 9%, en consonancia con los estudios poblacionales previos. Un prevalencia del 6% ó del 12% se consideran menos probables, y prevalencias del 2% ó 16% muy improbables. Se entrevistó a los 170 participantes y 10 confirmaron la presencia de EPOC (5.9%). Podría estudiarse la probabilidad de cada uno de los escenarios descritos dados los datos recogidos.

Tabla 1

Escenario	P(datos|θ)† (V)	Prob. a priori* (P)	V x P	Prob. posterior (V x P / S)
P(5.9%|2%)	0.002	0.1	0.0002	P(2%|5.9%)	0.005
P(5.9%|6%)	0.128	0.2	0.0256	P(6%|5.9%)	0.598
P(5.9%|9%)	0.041	0.4	0.0164	P(9%|5.9%)	0.383
P(5.9%|12%)	0.003	0.2	0.0006	P(12%|5.9%)	0.014
P(5.9%|16%)	0.000	0.1	0.0000	P(16%|5.9%)	0
		Suma=1	0.0428 (S)		Suma=1

^*: Se asume que la probabilidad de cada uno de estos escenarios es 0.1, 0.2, 0.4, 0.2, 0.1. La suma de estas probabilidades es 1, la probabilidad total de la distribución a priori. En este ejemplo, el estado no informativo sería aquel en el que se diera la misma importancia a los 5 escenarios: 0.2.
^†: La verosimilitud, o distribución de los datos obtenidos dado el supuesto de un θ concreto, seguirá una distribución binomial (se aportan los resultados)

El investigador tendría que concluir que para su población el escenario más probable es el de una prevalencia del 6%, siendo menos probable un 9%.

Otro aspecto de interés en el enfoque bayesiano es que todo resultado de un estudio (toda información) puede ser de interés. Dentro del estricto modelo frecuentista, la ausencia de significación puede llevarnos a pensar en ausencia de interés; una p = 0.12 puede quedar sin valor alguno. El análisis de esos mismos datos desde un enfoque bayesiano y con información obtenida de estudios previos podría llevarnos a conclusiones muy diferentes.

Esquemáticamente podemos representar todo lo dicho anteriormente de la siguiente forma:

 

 

Figura 3

Deseamos realizar una estimación del parámetro poblacional θ, para lo cual se cuenta con una información a priori (p(θ)) y unos datos obtenidos de la población, los cuales se distribuyen de una forma determinada (p(datos|θ), función de verosimilitud). El Teorema de Bayes nos permite realizar dicha estimación del parámetro poblacional. Compare este esquema con la Tabla 1 del ejemplo previo.

El enfoque bayesiano presenta notables ventajas en determinados campos:

• En general, el enfoque bayesiano puede tener importantes beneficios en el campo de los ensayos clínicos:
  • Reducción del tamaño muestral, mediante el análisis contínuo de la información disponible. O en caso contrario, si la variabilidad observada es elevada, el incremento de la muestra para poder llegar a conclusiones fiables
  • Modificación del diseño del estudio durante la ejecución del mismo, mediante la adecuada planificación
  • Monitorización de ensayos clínicos: Los ensayos clínicos, desde una perspectiva clásica, son diseñados para obtener determinadas diferencias entre los grupos de comparación con un diseño predeterminado:
    • Un planteamiento de hipótesis nula y alternativa
    • Unos errores alfa y beta
    • Un tamaño muestral calculado previamente
    • En un tiempo dado
    De forma que dentro del modelo frecuentista, sólo cumpliéndose dicho diseño podríamos llegar a conclusiones con un determinado grado de incertidumbre.
    Sin embargo, en momentos intermedios entre el inicio y el final programado para el ensayo tenemos de hecho información suficiente que, dentro de un enfoque bayesiano, puede ayudarnos a tomar decisiones sobre la necesidad o no de la continuación del estudio, bien porque se evidencia un claro beneficio en uno de los grupos o por el contrario, porque se evidencia un claro perjuicio. Son los análisis intermedios.
• Meta-análisis: Es un campo ideal para el uso del enfoque bayesiano, pues se trata de acumular información diversa para llegar a una valoración de conjunto sobre un determinado problema.
• Valoración de estudios locales con la información de otros estudios. El desarrollo de grandes estudios no siempre es posible, siendo más factible el desarrollo de estudios de menor tamaño. Sin embargo, estudios con tamaño muestral suficiente aunque reducido podrían ser tenidos bajo sospecha desde un enfoque clásico. El enfoque bayesiano nos permite utilizar la información facilitada por otros estudios para ratificar o refutar con los datos de nuestra población el conocimiento que se tenga sobre el problema estudiado. Por otra parte, el enfoque bayesiano también nos permite la adaptación de modelos epidemiológicos complejos, y fundamentados en los datos de amplias poblaciones, a nuestra población mediante el uso de los datos derivados de ella.
• Análisis de decisión.

Veamos ahora algunos ejemplos:

Ejemplo 1

Estudios previos estiman que la prevalencia de la enfermedad A en una población es de 16/100.000 hab, y la prevalencia del síntoma guía X de 120/100.000 hab. Se sabe además que un 30% de los enfermos que padecen la enfermadad A presentan el síntoma guía X. ¿Cuál sería la probabilidad de que un paciente que llegara a Urgencias con el síntoma guía X padeciera la enfermedad A?

P(A|X) = P(X|A) · P(A) / P(X) = 0.30 · 0.00016 / 0.0012 = 0.04

... es decir, un 4% de los pacientes con el síntoma guía X padecerán realmente la enfermedad A.

Como puede verse, este enfoque (ir del síntoma a la enfermedad) es clínicamente más relevante que el que podemos encontrar en cualquier tratado médico (en el que se va de la enfermedad al síntoma).

Ejemplo 2

Se plantea a una persona un juego en el que otra persona podrá lanzar varias veces uno o dos dados (el primero desconoce cuántos dados se lanzarán, pero siempre serán uno o los dos). Se le pregunta por el número de dados que se lanzan según los datos que obtienen con cada lanzamiento.
En este caso como información a priori se tiene el conocimiento del dado (6 caras). Se sabe que en el caso de que se lancen dos dados, ambos dados son independientes; por tanto la probabilidad de que salga un determinado número será la siguiente según se trate de uno o dos dados:

Distribuciones a priori
Distribución a priori para 1 dado
p(1|1 dado) = p(2|1 dado) = ... = p(6|1 dado) = 1/6
Distribución a priori para 2 dados
p(1|2 dados) = 0 p(2|2 dados) = p(12|2 dados) = 1/6 · 1/6 = 1/36 p(3|2 dados) = p(11|2 dados) = 2 · 1/6 · 1/6 = 2/36 p(4|2 dados) = p(10|2 dados) = 3 · 1/6 · 1/6 = 3/36 p(5|2 dados) = p(9|2 dados) = 4 · 1/6 · 1/6 = 4/36 p(6|2 dados) = p(8|2 dados) = 5 · 1/6 · 1/6 = 5/36 p(7|2 dados) = 6 · 1/6 · 1/6 = 6/36

Supongamos que en la primera tirada le informan que el resultado ha sido 5, y que el jugador se inclina por que es más probable que su amigo haya tirado 2 dados, con un 60% de probabilidad.

p(5|1 dado) = 1/6; p(5|2 dados) = 4/36
p(5) = p(5|1 dado) + p(5|2 dados) = 1/6 · 0.4 + 4/36 · 0.6 = 0.13
p(1 dado|5) = (1/6 · 0.4) / p(5) = (1/6 · 0.4) / 0.13 = 0.5
p(2 dado|5) = (4/36 · 0.6) / p(5) = (4/36 · 0.6) / 0.13 = 0.5

... lo que indica que con el conocimiento previo de la prueba y con los datos actuales es igualmente probable que se trate de uno o dos dados. Por tanto le pide al amigo que tire nuevamente los dados. Esta vez sale un 3. Ahora empleará como probabilidad a priori estos 50% obtenidos como probabilidad a posteriori del paso previo.

p(3|1 dado) = 1/6; p(3|2 dados) = 2/36
p(3) = p(3|1 dado) + p(3|2 dados) = 1/6 · 0.5 + 2/36 · 0.5 = 0.11
p(1 dado|3) = (1/6 · 0.5) / p(3) = (1/6 · 0.5) / 0.11 = 0.75
p(2 dado|3) = (2/36 · 0.5) / p(3) = (2/36 · 0.5) / 0.11 = 0.25

... lo que implica tras dos tiradas que es muy probable que en vez de dos dados, como creía en un principio, su amigo esté tirando dos dados. Pero le pide que tire una tercera vez, y ahora sale un 2.

p(2|1 dado) = 1/6; p(2|2 dados) = 1/36
p(2) = p(2|1 dado) + p(2|2 dados) = 1/6 · 0.75 + 1/36 · 0.25 = 0.13
p(1 dado|2) = (1/6 · 0.75) / p(2) = (1/6 · 0.75) / 0.13 = 0.95
p(2 dado|2) = (1/36 · 0.25) / p(2) = (1/36 · 0.25) / 0.13 = 0.05

... lo que le lleva a asegurar que su amigo ha estado tirando un único dado.

Ejemplo 3

Vamos a ver ahora cómo es útil este enfoque en el análisis de decisión.

El Ministerio de Sanidad y Consumo tiene dudas sobre el beneficio de vacunar a la población de una infección viral banal pero con una alta tasa de absentismo laboral. Se cree, por estudios previos, que el 60% de la población está inmunizada frente a la enfermedad. Se sabe además que la prueba diagnóstica tiene el siguiente rendimiento:

Rendimiento de la prueba
prob. de reacción [p(datos|θ)]	Reacción
	-	+	++	+++
Inmune	0.35	0.30	0.21	0.14
Vulnerable	0.09	0.17	0.25	0.49

Por último se sabe que el coste de no vacunar a un sujeto y que enferme es de 20€ (el valor de la vacuna y el coste del absentismo). Las restantes situaciones se consideran sin coste.

Resultados I
Coste de cada situación
p(θ|datos)·p(θ)	Reacción
	-	+	++	+++
Inmune	0.35·0.6=0.21	0.30·0.6=0.18	0.21·0.6=0.126	0.14·0.6=0.084
Vulnerable	0.09·0.4=0.036	0.17·0.4=0.068	0.25·0.4=0.1	0.49·0.4=0.196
p(datos) [suma]	0.246	0.248	0.226	0.28

Resultados II
p(θ|datos)·p(θ)/p(datos)	Reacción
	-	+	++	+++
Inmune	0.854	0.726	0.558	0.3
Vulnerable	0.146	0.274	0.442	0.7

Y si aplicamos el coste de cada circunstancia podremos ver el posible coste según la probabilidad de enfermear en función del tipo de reacción de la prueba diagnóstica.

Resultados III
	Reacción
	-	+	++	+++
Inmune y vacunado (x 8€)	6.83€	5.81€	4.46€	2.40€
Vulnerable y no vacunado (x 20€)	2.93€	5.48€	8.85€	14€
Decisión	No vacunar	No vacunar	Vacunar	Vacunar

Bibliografía:

1. Silva Ayçaguer LC, Benavides A. El enfoque bayesiano: otra manera de inferir. Gaceta sanitaria 2001;15:341-346.
2. Domenech JM. Fundamentos de diseño y estadística. Barcelona: Signo; 2001.
3. Silva Ayçaguer LC, Muñoz A. Debate sobre métodos frecuentistas vs bayesianos. Gaceta Sanitaria 2000;14:482-494.
4. Silva Ayçaguer LC, Benavides A. Apuntes sobre subjetividad y estadística en la investigación en salud. Rev Cubana Salud Pública 2003;29:170-173.

Ficha bibliográfica

Título:

Inferencia estadística según el modelo bayesiano

Direcci n:

http://epidemiologia-estadistica.blogspot.com.es/2013/02/inferencia-estadistica-segun-el-modelo_19.html

Descripcin:

Se describen los conceptos básicos para poder entender el funcionamiento de la inferencia bayesiana y sus ventajas e inconvenientes frente al modelo frecuentista o clásico. Se aportan ejemplos.

Palabras clave:

estadística bayesiana; inferencia; análisis de decisión, probabilidad a priori

Código de idioma:

es

Autor:

Fco. Javier Caballero Granado

Editor:

Fco. Javier Caballero Granado

Derechos:

Fco. Javier Caballero Granado

Fecha de creaci n:

2006-03-20

Modificado:

2007-02-13

Forma parte de:

Notas sobre estadística

Cómo citar:

Caballero-Granado FJ. Inferencia estedística según el modelo bayesiano [en línea]. Caballero-Granado FJ Ed. Creado el 20/03/2006; actualizado el 13/02/2007. Disponible en web: http://epidemiologia-estadistica.blogspot.com.es/2013/02/inferencia-estadistica-segun-el-modelo_19.html [consultado el ...]

Inferencia estadística según el modelo frecuentista

Cuando deseamos estudiar una determinada característica de una población concreta, ya sea una cualidad, una enfermedad, etc, no nos es posible trabajar con toda esa población (no tendríamos ni tiempo ni recursos económicos suficientes para la recogida de datos). Por ejemplo, si queremos estudiar la relación entre tabaco y cáncer de pulmón, no podemos estudiar a todos los fumadores de un país para hacer un estudio prospectivo, ni tampoco estarán a nuestra disposición todos los pacientes con cáncer de pulmón para hacer un estudio retrospectivo. Es por ello necesario tomar una muestra que sea representativa de la población que queremos estudiar.
No es el momento de estudiar cómo debe ser la recogida de esta muestra, pero valga aquí decir que precisaremos tomar una muestra aleatoria, mediante una técnica u otra, pues la única forma por la cual nos garantizaremos que la muestra que tomemos será representativa de la población que queremos estudiar y evitaremos la presencia de sesgos de selección. Podremos entender pues, que la muestra que vamos a seleccionar para nuestro estudio no es la única muestra que podríamos tomar, y que si repitiéramos la selección de la muestra una y otra vez, en cada ocasión la misma tendría una composición diferente de indivíduos. De la misma forma, si realizáramos en cada una de estas muestras la medición de una característica (porcentaje del color de ojos azules, presencia de tabaquismo, media de edad, etc), ésta no nos daría el mismo resultado. Sabemos así que al tomar una muestra de la población objeto de estudio y realizar una medición estamos cometiendo un error (llamado error aleatorio), cuya magnitud dependerá, lógicamente, del tamaño de la muestra: a mayor tamaño, menor error. No podemos, sin embargo, caer en la tentación de pensar "entonces, mientras más mejor"; existen técnicas para saber el número mínimo de una muestra para realizar un estudio según un planteamiento previo a la realización del mismo.
La inferencia estadística es el conjunto de técnicas estadísticas que nos permiten llegar a conclusiones sobre una población a partir de una muestra de dicha población.
El objetivo de las técnicas de inferencia estadística es contrastar (esto es, decidir o evaluar), dos hipótesis acerca del parámetro de interés. Estas dos hipótesis son la hipótesis nula (llamada H₀) y la hipótesis alternativa (llamada H₁).
En el momento de la decisión podemos cometer dos tipos de error. Podemos rechazar la hipótesis nula, siendo esa hipótesis la verdadera (error tipo I o error α), o bien podemos rechazar la hipótesis alternativa siendo la misma verdadera (error tipo II o error β). La probabilidad complementaria del error tipo II (1 - β) es el llamado poder del contraste.
Se debe colocar como hipótesis nula aquélla que no interesa al investigador, mientras que la hipótesis alternativa será la que el investigador quiere demostrar. Esto es así pues rechazar la hipótesis nula es lo mismo que decir que hemos llegado a tener pruebas de que la misma es falsa. Por el contrario no poder rechazar la hipótesis nula es lo mismo que decir que no tenemos pruebas suficientes como para llegar a saber que la hipótesis nula es falsa, y por tanto, tampoco tenemos la suficiente certeza de que dicha hipótesis sea cierta.
Supongamos que deseamos conocer algún parámetro poblacional, por ejemplo la edad media de una población. En el contexto de la estadística clásica (frecuentista), podríamos extraer al azar múltiples y diferentes muestras representativas de forma sucesiva y determinar el estimador más apropiado en cada una de esas muestras. Para este caso, el estimador más apropiado para la media poblacional es la media muestral. Cada una de las medias de estas muestras tomarían un determinado valor diferente para cada muestra (o lo que es lo mismo, el estimador es tratado como una variable en sí mismo). Suponiendo la normalidad de la variable "edad", los valores que irían tomando estas medias muestrales se distribuirían según una curva de Gauss (algunos de estos valores se darían con mayor frecuencia y otros con menor frecuencia). El área bajo dicha curva de distribución de frecuencias del estimador es la probabilidad total, es decir, la unidad.

 

Por tanto, los valores que podrían tomar estas medias muestrales se concentrarían en la zona central de la curva de distribución (es decir, serían los valores más frecuentes del estimador)

 

Nos centraremos ahora en el extremo derecho de esta curva

 

Cualquier valor que tome la media muestral dejará por encima de él un área bajo la curva de un determinado valor. Supongamos que tenemos un valor X₀ que deja el 95% del área por debajo y el 5% del área por encima.

 

Esto es lo mismo que decir que cualquier valor de media muestral por encima de X₀ es un valor “muy raro” de la distribución (lo encontraríamos con una frecuencia inferior al 5%). Supongamos también que deseamos contrastar nuestras hipótesis nula y alternativa con un error máximo del 5% (error α o error tipo I). Entonces, X₀ sería ese valor crítico tal que si obtenemos una muestra y efectuamos nuestro experimento (medición de la media) bajo la perspectiva de la hipótesis nula, el obtener cualquier valor X₂ de media por encima de X₀ nos llevaría al rechazo de la hipótesis nula y la aceptación de la hipótesis alternativa.

 

 

 

Así mismo, si realizada la experiencia obtuviéramos un valor X₁ menor que X₀, o lo que es lo mismo, un área bajo la curva para X₁ mayor que α, esto nos llevaría a no rechazar la hipótesis nula.

Este valor de probabilidad, de área bajo la curva por encima de X₁, es lo que llamamos valor de p. Es decir, p es la probabilidad de que un valor tan extremo o más que el obtenido de nuestros datos pueda observarse en la población si la H₀ es cierta.
Un resumen de lo que hemos hecho hasta ahora se aprecia en la siguiente figura

 

Tenemos una población de la que desconocemos un parámetro que nos interesa conocer; para ello extraemos al azar una muestra representativa de la misma; a partir de esta muestra obtenemos el estimador muestral más apropiado para el parámetro poblacional que se desconoce; planteamos la hipótesis de trabajo que deseamos contrastar, y bajo un modelo de probabilidades en el que el parámetro poblacional es considerado constante y el estimador (datos muestrales) es considerado variable determinamos un valor de p; con el resultado de p realizamos conclusiones acerca de nuestra hipótesis, es decir, acerca del parámetro poblacional.
Dado que no es posible dar un valor exacto de los parámetros poblacionales desconocidos, sino sólo una aproximación a los mismos a través de las muestras que extraemos de la población, siempre será más adecuado proporcionar intervalos de confianza que estimaciones puntuales. Un intervalo de confianza al 95% es un rango de valores tal que, si repitiéramos infinidad de veces el experimento, el 95% de las estimaciones del parámetro poblacional estarían contenidas en él. Para la construcción de intervalos de confianza utilizamos nuestra estimación y el error estándar del estimador que hayamos empleado. El error estándar es el grado de error que toleramos en nuestra estimación. Estos son algunos errores estándares frecuentemente usados:

• Proporción (muestras grandes):

• Media:

 

Como podemos observar, el error estandar es inversamente proporcional al tamaño muestral, o lo que es lo mismo, conforme aumentamos el tamaño muestral nuestra estimación es más exacta, mientras que con muestras pequeñas el grado de incertidumbre llega a ser importante.
Continuemos construyendo nuestro intervalo de confianza. Éste debe contener al menos el 95% de las posibles estimaciones (p < 0.05). Si nuestra muestra es sufiencientemente grande y nuestro estimador sigue una distribución normal, sumaremos y restaremos a nuestra estimación puntual 1.96 veces el error estándar del estimador (en una curna de Gauss con media 0 y desviación típica 1 el 95% de su área bajo la curva se encuentra entre -1.96 y +1.96). Si siguiera una distribución t de Student (por ejemplo para medias de muestras de muestras de menos de 30 indivíduos), nuestro intervalo de confianza sería la estimación puntual más y menos t_n-1;0.05 veces el error estándar (siendo t_n-1;0.05 el valor de una t de Student en una muestra de n indivíduos para un valor de p de 0.05).
Pues bien, contrastar nuestra hipótesis nula y alternativa no será más que comprobar si nuestro intervalo de confianza incluye o no el valor que nos interese.
Observemos la siguiente figura. En ella vemos un ejemplo en el que se contrasta el valor del peso de los recién nacidos en una población. El valor que se desea contrastar es 3.2 Kg. Nuestra estimación realizada a partir de una muestra de dicha población es 2.8 Kg. Como ya sabemos, el error estándar de la media será tanto mayor cuanto menor sea el tamaño muestral. En la figura vemos como para dos tamaños muestrales diferentes nuestro intervalo de confianza varía en su amplitud, y mientras que con el inferior (n = 20), contiene el valor que se está contrastando, lo que no llevaría a no rechazar la hipótesis nula (p > 0.05), con el intervalo superior (n = 100), el valor contrastado está fuera del intervalo de confianza, lo que nos llevaría al rechazo de la hipótesis nula (p < 0.05).

 

Por lo tanto, una característica de p es que su valor depende del tamaño de la muestra a partir de la cual se determina: a mayor tamaño muestral mayor es la probabilidad de encontrar diferencias significativas entre los grupos que se comparan. De ahí la importancia de que en todo estudio deba realizarse el cálculo del tamaño muestral necesario en base a las caractrísticas de dicho estudio con anterioridad a la recogida y el análisis de los datos.

Ficha bibliográfica

Título:

Inferencia estadística según el modelo frecuentista

Dirección:

http://epidemiologia-estadistica.blogspot.com/2013/02/inferencia-estadistica-segun-el-modelo_17.html

Descripción:

Se describen los conceptos necesarios para saber el desarrollo intelectual que subyace a la inferencia estadística clásica y se aportan ejemplos.

Palabras clave:

estadística; inferencia; valor p; error estándar; hipótesis nula; hipótesis alternativa

Código de idioma:

es

Autor:

Fco. Javier Caballero Granado

Editor:

Fco. Javier Caballero Granado

Derechos:

Fco. Javier Caballero Granado

Publicado:

2006-02-30

Modificado:

2007-02-17

Forma parte de:

Notas sobre estadística

Cómo citar:

Caballero-Granado FJ. Inferencia estedística según el modelo frecuentista [en línea]. Caballero-Granado FJ Ed. Creado el 30/02/2006; actualizado el 17/02/2007. Disponible en web: http://epidemiologia-estadistica.blogspot.com/2013/02/inferencia-estadistica-segun-el-modelo_17.html [consultado el ...]